撲克牌版的 「公鑰夾帶部分私鑰」 密碼破解術

[2013/12/22 補充： 啊！ RSA 的後門不只是理論上存在於亂數產生器當中。 最新的 Snowden 解密證實： （中文） NSA 真的以三億台幣買通 RSA公司， 在其產品內植入 Dual EC 後門。 路透社、 衛報、 簡中。]

監聽， 是很受統治者歡迎的技術。 40 年前美國總統 尼克森 頗好此道， 也因此羞愧下臺。 今天的美國政府掌握更先進的科技， 並藉反恐、 打擊犯罪之名， 更全面地對國內外公民違法監聽。 Edward Snowden 因為在今年六月間揭發 NSA （國安局） 的監聽弊案而 獲頒吹哨者獎， 但後續記者及電腦專家仍在持續分析尚未爆完的資料。 最近又有好幾彈爆開， 其中一彈嚇死人： 美國國安局幾乎可以破解所有網路加密協定 （中文）。 這引發大家熱烈討論， 連 噗浪 都很熱鬧。 即使 紐約時報 跟 華盛頓時報 都報出來了， 即使 資安專家都因此而跳出來呼籲必須更改網安標準， 很多人還是不相信 NSA 辦得到。 NSA 到底可能採取哪些神奇的方式破解密碼？ 有興趣的朋友可以幫忙摘譯 register 所推薦的 資安教授 Matthew Green 分析文。 （我也大推！） 本文只針對其中一種很明確可行的可能性， 拿撲克牌當比喻， 讓大家知道： 當你所採用的加解密軟體來自一家 「與 NSA 過從甚密的廠商」 而你又看不到原始碼的時候， 「NSA 可以破解你的密碼」這完全是辦得到的事。

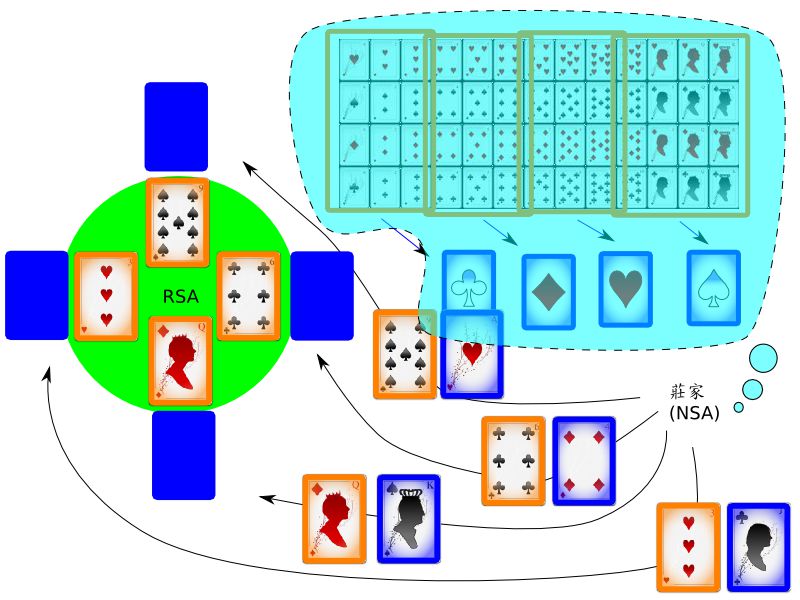
把網路上的加解密活動極度簡化， 想像成是一桌撲克牌局。 這個牌局的遊戲規則細節我們就省略了， 只需要知道：

1. 有兩付撲克牌， 一副是藍色， 另一副是橘色。
2. 遊戲一開始， 莊家會發給每個人一張藍牌、 一張橘牌。
3. 每個人把手上的橘牌攤在牌桌上， 但藍牌不給別人看。

如果你對於這兩張牌所代表的詳細意義有興趣， 可以參考 白話版的非對稱式加解密； 但就本文而言， 其實只需要知道： 橘牌代表加解密演算法當中的公鑰 （大家都看得見）， 而藍牌則代表私鑰 （只有自己看得見）。

現在的問題是： 莊家有沒有可能知道每個人手中的藍牌是哪張？ 如果莊家照規矩來， 雖然發牌的時候他一定會看見牌， 但理論上他不應該記牌。 但是如果他發牌的時候動一點手腳， 自己加一點潛規則進去， 把藍牌的資訊藏到橘牌裡面去， 那他就比不知情的玩家要佔一些便宜了。 例如他發牌的時候， 可以先抽一張橘牌， 然後 根據橘牌的數字大小來決定要發什麼花色的藍牌給玩家。 更具體地舉例， 比方他自己暗中決定：

1. 如果橘牌是 A 或 2 或 3， 那麼他就不斷地重抽藍牌， 直到抽到梅花， 才把它跟橘牌一起發給玩家。
2. 如果橘牌是 4/5/6， 那就一定要抽到一張方塊的藍牌才發牌。
3. 如果橘牌是 7/8/9， 那就一定要抽到一張紅心的藍牌才發牌。
4. 如果橘牌是 10 或人頭， 那就一定要抽到一張黑桃的藍牌才發牌。

因為橘牌攤在桌上， 所以大家都看得見； 但是因為只有莊家知道發牌的潛規則， 所以只有他可以從攤在桌面上的橘牌推測出蓋著的藍牌的花色。

以上就是我對這篇論文 "Simple Backdoors for RSA key generation" 的 「撲克牌比喻版」 白話翻譯。 當然， 真實的狀況要複雜很多， 理解上述比喻之後， 還需要略微修正如下。

「莊家」 在真實世界裡， 就是密碼產生器/亂數產生器。 拿 「NSA 要求微軟安裝在 Windows 裡的後門」 來說， 如果運作方式真的類似本文所述的話， 它也不太可能記牌 （記住每位 Windows 用戶所產生的所有公私鑰）， 因為 「每當金鑰一產生就出現 （回傳 NSA 的） 網路活動」 太容易被識破。 所以採取本文的策略比較合理可行 -- 一般人不會想到私鑰的部分訊息會被藏在公鑰裡、 更不會想到只洩漏私鑰的部分訊息， 密碼就會被完全破解。

從一副撲克牌當中抽一張， 只能傳遞不到 6 個 bits 的資訊 （52 < 64 = 2⁶）， 雖然比 2.3 bits 的教學品保量化指標 更有意義一點， 但跟實際應用上幾十或幾百個 bits 的資訊還是差很多。 在上述的比喻中， 莊家很老千地把 （理應是私密的） 藍牌其中 2 個 bits 的資訊 （2² = 4 種花色） 暗藏到橘牌的 5.8 個 bits 裡面去。

在實際的 RSA 加解密演算法當中， 藍牌跟橘牌之間本來就不能任意組合、 莊家 （密碼產生器） 本來就合理地必須篩選出某些有意義組合的一雙 「藍牌/橘牌」。 也因此， 會浪費掉一些 bits。 RSA Security 公司表示： 1024 bits 的 RSA 密碼， 大約只有 80 bits （完全自由隨意亂碼的） 對稱加密密碼的強度； 3072 bits 的 RSA 密碼， 大約等同於 128 bits 完全亂碼的強度。

「玩了一陣子之後， 莊家的潛規則會不會被觀察力敏銳的玩家發現呢？ 例如玩家可能發現： 為什麼每當我拿到點數小的橘牌時， 藍牌就一定是梅花？」 因為真實世界的 bits 數太多， 可以排列組合的方式太多， 所以莊家可以採用很複雜的潛規則把資訊打很亂地藏到橘牌裡， 讓玩家很難看出與正常隨機發牌有何不同。

「只知道藍牌的花色， 還是無法精確地指出藍牌是哪一張啊！ （所以無法破解密碼）」 嗯， 到這裡， 就幾乎必須把比喻丟掉了。 Simple Backdoors 論文其實是建立在 An attack on RSA given a small fraction of the private key bits （及其他更數學、 我沒讀） 的結果之上。 如前所述， 藍牌與橘牌之間其實並不是完全隨意組合。 也就是說， 就算莊家不耍老千， 任何人從桌面上對手的橘牌還是可以稍微推算一下他手中可能有哪些藍牌、 不可能是哪些藍牌。 如果進一步知道藍牌更多一點資訊， 就更可以縮小範圍了。 這篇 attack 論文指出： 只要可以取得藍牌 （bits 數） 1/4 的資訊， 那麼要精確指出藍牌到底是哪一張， 就變得 「相對很簡單」。 （所需破解時間從 exponential time 大幅降到 polynomial time） 他們並且真的跑程式測試， 在 500MHz 的 Intel P3 機器上試著破解 1024 bits 的 RSA 密碼 （假設已知其中最高的 256 bits） 只需要 21 小時。 如果說原先破解 RSA 的困難度就像想要出大氣層旅遊一樣 -- 不是不可能， 但你我做不到 -- 那麼 「已知部分密碼」 版的破解困難度就像花個一兩千塊搭高鐵旅遊一樣輕鬆。

這裡雖然是舉 RSA 為例， 但我相信網路上一定還可以找得到更多破解其他 「非對稱式加解密」 的論文。 當然， 像是 RSA 這類歷經長時間驗證的加解密演算法， 都不太可能被徒手直接攻破 -- 比較可能是在 「部分機密被偷偷巧妙洩漏」 的前提之下， 才會被破解。 而最簡單的 「偷偷巧妙洩漏」 方式， 就是如本文所說， 把私鑰的一部分資訊藏在公鑰裡面。 最有可能被惡意動手腳的地方， 就是密碼產生器與亂數產生器， 而美國 NSA 與 FBI 等等情治單位， 過去不斷在這方面出手惹議， 早為關心資安人士知悉。 小格先前提及的兩個案例 NSA 要求微軟在 Windows 裡暗藏的 DUAL_EC_DRBG 後門 以及 OpenBSD 被懷疑遭 FBI 植後門 （但後來證實並沒有） 最終都追蹤到這個地方。 差別在於： OpenBSD 的原始碼攤在陽光下， 所以大家可以仔細檢查可疑的地方； 而 Windows 的程式碼看不見， 所以用戶就只好自求多福了。 我們一直強調： 為什麼社會應該要採用自由軟體/開放原始碼軟體？ 除了免費跟好用之外， 還有其他更重要的原因 -- 資訊安全也是其中之一。 採用開放原始碼軟體， 並不必然就 100% 安全； 但若採用看不見原始碼的軟體， 那根本就不必談什麼資訊安全了。

[2017/10/8 巧遇這篇 直接針對 Dual EC DRBG 的英文白話解說文。]

* * * * *

（本文也刊載於 泛科學、 T 客邦）

手邊沒電腦； 口頭推薦本文嗎？ 可以請您的朋友搜尋 「撲克牌 公鑰」 或 「撲克牌 夾帶私鑰」。